이 글은 JWT에 대한 개념을 다루지 않습니다. JWT의 개념을 숙지한 다음 해당 글을 읽으시면 더 많은 도움을 받을 수 있습니다.
JWT 암호화 알고리즘, 왜 중요할까?
JWT는 인증/인가 시스템에서 널리 사용되는 토큰 포맷이다.
이러한 JWT를 발급하고 인증하는 과정에서, 암호화 알고리즘을 선정하는 것은 아래 요소들에 큰 영향을 미친다.
- 보안성: 키 유출 시 얼마나 위험한가? 얼마나 오래 안전한가?
- 성능: 토큰의 발급 및 검증 속도는 얼마나 되는가?
- 확장성: 다수의 서비스가 검증에 참여할 수 있는가? 새로운 서비스가 검증을 수행하고자 할 때의 난이도는 어떠한가?
- 운영 난이도: 구현이 쉬운가? 디버깅 및 문제 추적이 쉬운가? 키 관리와 배포가 얼마나 쉬운가?
그리하여 이번 글에서는 JWT를 다룰 때 주로 사용되는 암호화 알고리즘들의 구조와 동작 방식, 장단점 등을 인증 서버의 개발 및 운영자 관점에서 살펴보고자 한다.
암호화 알고리즘의 목적에 따른 분류
JWT는 암호화 방법에 따라 크게 2가지로 분류된다. 바로 서명(Signature) 기반과 암호화(Encryption) 기반이며, 어떤 방법을 선택하느냐에 따라 JWS(Json Web Signature)와 JWE(Json Web Encryption)로 불린다.
서명 기반은 암호화를 통해 ‘무결성’, ‘발급자의 신원’을 보장하는 것을 목적으로 한다. 즉, 토큰이 변조되지 않았으며 올바른 발급자로부터 발급되었음을 보장하는 것을 목적으로 한다. 이러한 서명 기반 암호화 알고리즘으로는 HMAC, RSA, ECDSA 등이 있다.
암호화 기반은 암호화를 통해 ‘비밀성’을 보장하는 것을 목적으로 한다. 즉, 데이터가 제3자에게 노출되지 않도록 내용물을 숨기는 것을 목적으로 한다.
본 글에서는 서명 기반 토큰인 JWS를 만들기 위해 사용하는 암호화 알고리즘들을 중점적으로 다룰 것이며, JWE에 대해서는 다루지 않는다. (JWE는 나도 아직 안 써봐서.. 나중에 쓸 일이 생기면 그 때 정리하겠다!)
서명 기반 알고리즘 (JWS)
서명의 목적은 ‘비밀성’이 아님에 다시 한 번 유의할 것! 이 알고리즘들은 메시지 내용물을 보호하는 것을 목적으로 하지 않는다.
앞에서 언급했듯, 서명 기반 암호화에는 아래의 세 가지 알고리즘이 주로 사용된다.
- HMAC (HS256 등)
- RSA (RS256 등)
- ECDSA (ES256 등)
각 예시 알고리즘의 약자에 붙는 S256은 SHA-256을 의미한다. 위 알고리즘들은 모두 해시 함수를 사용하는데, 이들은 그 중에서도 해시 함수로 SHA-256(256 bit의 고정된 임의 문자열을 출력하는 해시 함수)를 채택하고 있는 알고리즘 기법들이라고 이해하면 된다.
이제 각 알고리즘들의 동작 방식과 장단점을 분석해보고 언제 어떤 알고리즘을 채택하면 좋을지 알아보자.
HMAC (Hash-based Message Authentication Code)
정의
HMAC은 암호화 주체, 검증 주체 간 미리 공유된 키(대칭키)를 기반으로 해시 함수를 적용해 암호문을 생성하는 기술이다.
여기서 MAC이란 원본으로부터 생성 가능한 암호문을 말하며, 이 인증 코드를 통해 원본 메시지의 무결성을 검증할 수 있다.
동작 방식
HMAC의 내부 동작은 아래와 같다.
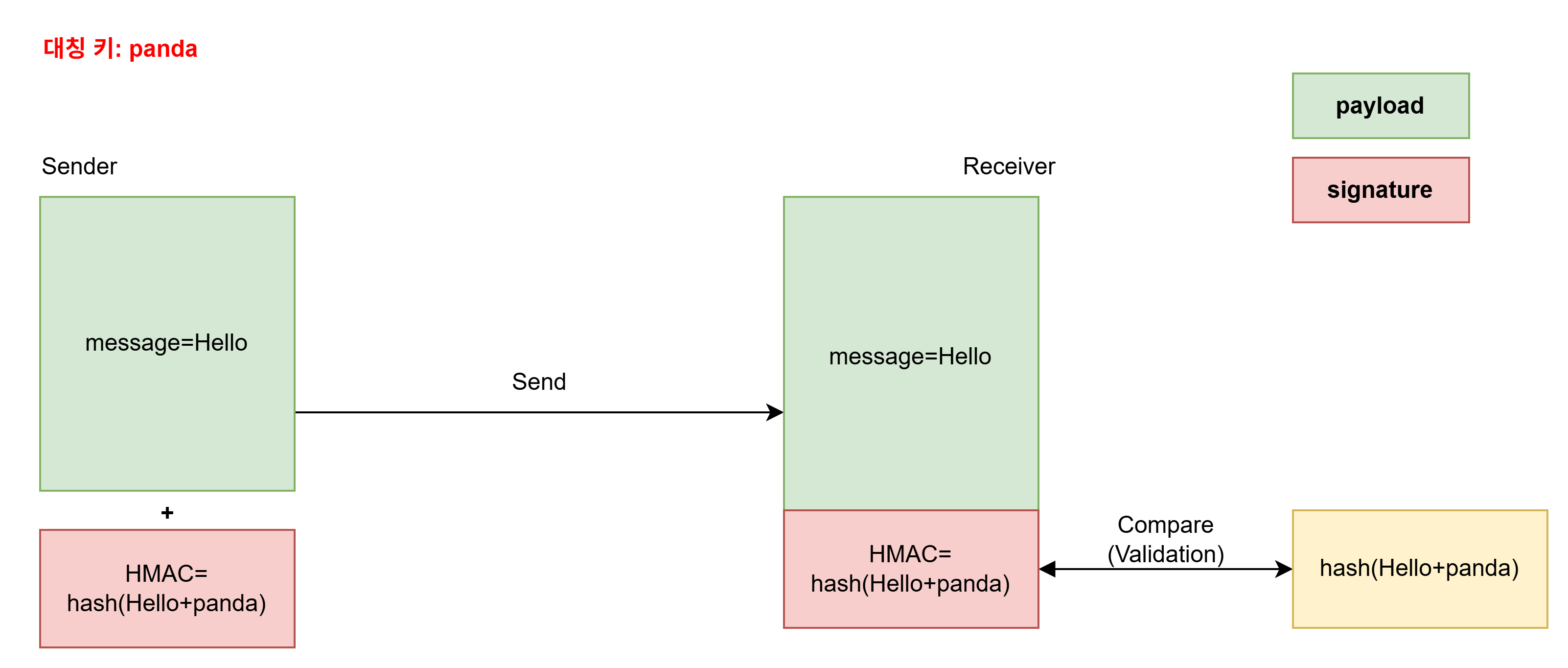
- (메시지의) 송신자와 수신자는 사전에 미리 협의한 비밀키를 보관한다.
- 송신자는 메시지+키를 기반으로 생성한 해시(HMAC)를 원본 데이터와 함께 전송한다. (이 과정에서 해시 함수로 SHA-256이 사용하는 것이 HS256(HMAC+SHA-256) 알고리즘이다.)
- 수신자는 원본과 HMAC을 받아 원본+키를 해시 함수에 통과시킨 것이 HMAC과 동일한지 확인함으로써 무결성을 검증한다.
즉 여기서 Signature 역할을 하는 것은 메시지+키에 대한 해시 값인 HMAC이다.
장단점
HMAC은 구현 방법이 아주 간단하고, 속도가 빠르다는 장점이 있다. HMAC은 토큰의 서명 및 검증에 있어 이 글에서 소개할 3개 알고리즘 중 가장 빠른 속도를 보인다.
하지만, 대칭키 기반이기 때문에 키를 탈취당하면 전체 시스템의 보안이 붕괴된다는 문제점이 있다.
또한, 검증을 수행해야 하는 모든 서비스가 이 대칭키를 비밀리에 잘 공유받아야 해서, 키 관리의 어려움이 있으며 이는 곧 확장성 저하를 야기한다.
RSA
정의
RSA는 비대칭키(공개키/개인키)를 사용하며 개인키로 서명해 발급하면 인증 주체가 공개키를 통해 검증하는 알고리즘으로, 컴퓨터가 큰 정수를 소인수분해하는 것의 어려움에 기반을 둔다.
참고로 RSA는 특정 의미를 가지는 약자는 아니고, 해당 알고리즘의 발명자들의 이름에서 딴 약자라고 한다.
키 생성 방식
RSA 키의 생성에는 아래의 값들이 관여한다.
- p, q: 두 소수
- N: p와 q를 곱한 값
- p, q가 소수이기 때문에 ϕ(pq) = ϕ(N) = (p-1)(q-1)
- e: ϕ(N)보다 작고 ϕ(N)과 서로소인 정수 (공개 지수. 보통 3, 65537 같은 페르마 소수를 사용)
- 위의 값들로부터 ed = 1 mod ϕ(N) 를 만족하는 정수 d를 계산 (개인 지수)
이로부터 공개키 (e, N) 과 개인키 (d, N)을 획득할 수 있다.
e, d, N에 대하여 c = m^e mod N, m = c^d mod N을 만족하기 때문에, 하나로 암호화한 것을 다른 하나로 복호화할 수 있는 것이다.
이 모든 것을 완전히 이해하거나 암기하지 않아도 RSA 키를 생성하는 도구들이 잘 되어 있어서 우리가 직접 p, q를 선정하고 키를 만들 일은 거의 없으니 문제가 없다. 하지만, p와 q를 알고 e 또는 d를 알면 사실상 공개키와 비밀키를 모두 알아낼 수 있다는 점에는 유의해야 한다. 보통 공개키는 배포되기 때문에 제3자가 접근할 가능성이 있다고 고려하면 e와 N은 노출되는 것이나 다름 없으니, p와 q가 노출되지 않도록 키를 생성한 이후에는 p와 q를 파기하는 것이 안전하다. (p와 q는 아주 큰 값이기 때문에 N으로부터 이를 역추적하는 것은 아주 어렵다.)
동작 방식
RSA의 동작 방식은 아래와 같다. 아래 연산 과정을 숙지하고 살펴보자.
서명: s = hash(m)^d mod N
검증: m = s^e mod N

- (메시지의) 송신자는 대칭키를 생성하고 자신의 비밀키로 Signature(s)를 생성한다.
- 수신자는 수신자의 공개키로 Signature를 검증하여 무결성을 검증한다.
장단점
RSA는 비밀키만 탈취당하지 않으면 되는데 암호화 주체만 비밀키를 가지면 되기 때문에 비교적 안전한 알고리즘이다. 검증 주체는 암호화 주체가 사전에 배포해 둔(접근 가능한) 공개키를 획득하여 검증을 수행할 수 있으며, 이 공개키는 제3자에게 노출되어도 검증만 가능한 키이므로 큰 보안 문제가 발생하지 않는다.
또한, RSA 알고리즘은 아주 오랜 기간 대표 알고리즘 자리를 지켜왔던 만큼 다양한 라이브러리/플랫폼이 지원되기 때문에, 구현 난이도나 잘못된 구현으로 인한 위험성도 낮은 편이다.
하지만, RSA는 3개 알고리즘 중 가장 느린 서명/검증 속도를 보인다. 또한, 공개키와 비밀키의 크기가 큰 편이며(2048bit 이상), Signature의 길이 또한 최소 256bit 이상으로 긴 편이다.
ECDSA (Elliptic Curve Digital Signature Algorithm)
정의
ECDSA도 RSA와 마찬가지로 비대칭키를 사용하는 알고리즘으로, 타원 곡선의 이산 로그 문제(ECDLP)의 어려움에 기반을 둔다.
키 생성 방식
ECDSA 키의 생성에는 아래의 값들이 관여한다.
- Curve: 연산이 일어나는 공간(field)을 정의. 방정식으로 나타남
- G: 기준점(base point). 타원 곡선 위의 정해진 시작 지점 (x, y)
- n: nG=0(무한점)을 만족하는 최소값으로, 아주 큰 소수
- d: [1, n-1] 사이에서 무작위로 선택한 정수로, 개인키 역할을 함
- Q: d와 G를 곱한 값으로(스칼라 곱 d · G), 공개키 역할을 함
- k: [1, n-1] 사이의 난수. 서명에 관여하며 매 서명마다 새로운 값을 선정
즉, d와 Q가 실질적 키 역할을 함을 알 수 있다. 그렇다면 RSA처럼 ECDSA도 공개키 Q와 G가 노출되면 비밀키를 계산할 수 있을까? 그렇지는 않다. 대신 nonce k 값을 그대로 사용하고 이 값이 노출된다면 비밀키를 추출하는 것이 가능하니, 서명 시 반드시 안전한 난수 k 또는 deterministic nonce(RFC 6979)를 사용해야 한다.
동작 방식
동작 방식은 RSA와 동일하다. 단, 서명과 검증에 아래와 같은 연산이 사용된다.
서명
- 최종 서명의 형태는 (r, s)
- [1, n-1] 사이의 난수 k에 대하여 k · G = (x1, y1) 계산 (k는 매 서명마다 새로 선정)
- r = x1 mod N (이 때 r = 0이면 k를 다시 선정)
- s = k^-1(hash(m) + r · d) mod n
검증
- (x1’, y1’)를 구해 (r, s)와 비교
- w = s^-1 mod n
- u1 = z · w mod n
- u2 = r · w mod n
- 곡선 위 u1 · G + u2 · Q = (x1’, y1’)
장단점
RSA보다 더 짧은 키로 동일한 보안 수준을 제공할 수 있다. 무려 ECC 256-bit가 RSA 3072-bit 수준이라고 한다.
RSA보다 키와 서명의 크기가 훨씬 작으며, 서명 및 검증 속도도 더 빠르다.
하지만, ECDSA는 구현 난이도가 높고, RFC 표준을 엄격히 준수해야 한다. 그렇지 않으면 치명적 취약점이 발생할 수 있다.
또한, 디버깅 및 문제 추적 난이도가 높아, RSA에 비해 운영 난이도가 높은 편이라고 볼 수있다.
어떤 알고리즘을 사용하면 좋을까?
첫 단락에서 언급한 요소들에 대해, 3가지 알고리즘은 아래와 같은 순위를 가진다.
- 보안성: ECDSA > RSA > HMAC
- 성능: HMAC > ECDSA > RSA
- 확장성: RSA > ECDSA > HMAC
- 운영 난이도 (낮은 순): HMAC > RSA > ECDSA
빠르고 간단한 것은 단연 HMAC이지만, HMAC은 대칭키를 사용함에서 오는 명확한 한계점과 취약점이 존재한다.
RSA와 ECDSA는 비대칭키(공개키-비밀키)를 사용해 HMAC이 갖는 취약점은 개선하였으나, 속도와 난이도 간 Trade-off를 갖는다.
차세대 암호화 알고리즘으로 주목받는 것은 ECDSA이나, 아직 RSA만큼 자료나 라이브러리/플랫폼 구축이 잘 되어있지 않아 섣불리 도입하기에는 부담이 될 수 있다.
RSA가 ECDSA에 비해 성능이 떨어지는 것은 사실이지만 트래픽이 폭발적인 서비스가 아니라면 크게 병목이 될 수준은 아니기 때문에, 여전히 RSA를 채택하는 인증 서비스도 많다.
그래서 정리하자면 아래와 같은 사항을 고려해서 알고리즘을 선택하면 좋다!
- 인증 주체가 단일 서버이거나 아주 적고, 확장될 가능성이 거의 없다면 -
HMAC - 여러 서비스에서 검증이 필요하고, 확장될 여지가 있으며, 속도보다는 안정성이 최우선 -
RSA - RSA와 동일 조건에서 좀 더 고성능이어야 하고, 운영 난이도를 감수할 수 있는 경우 -
ECDSA

